堆结构

GinShio 收录于类别和系列数据结构与算法分析

08-25 04-07 约 1129 字预计阅读 6 分钟

系列 - 数据结构与算法分析

模型

优先队列 (priority queue) 的 ADT 与 queue 类似，它们都提供了基本的 enqueue 与 dequeue 操作。但是 priority queue 可以在 dequeue 时将数据按照一定顺序弹出队列，而不是 FIFO。我们这里主要讨论每次出队最小的元素 (即 delete_min)，如果你希望进行其他一些有规范的操作，方法与这类似。

显然 priority queue 有一个朴素解，那就是在每次 delete_min 时遍历整个存储单元，找到最小的元素并删除，其时间复杂度 \(\mathcal{O}(N)\) ，当然插入元素的时间复杂度会好很多，只需要 \(\mathcal{O}(1)\) 。当然你也可以将其反过来，在插入时就找到最小的元素。

显然这是无法接受的，即使是利用前几篇中介绍过的 AVL 树都可以将其时间复杂度压缩到 \(\mathcal{O}(\log_{}{N})\) 。不过这有点太过分了，平衡 BST 的很多操作可能是用不上的，而且为了优先队列再实现一个平衡树实在是太难为人了。

我们将要介绍的工具叫做 二叉堆 (binary heap)，用以实现有限队列。但是需要注意的是， 堆 (heap) 这里指的是一种数据结构，而非操作系统中用以分配动态内存的地方。

二叉堆

结构性质

binary heap 是一棵被完全填满的二叉树，或者说是一棵 complete binary tree。由于 complete binary tree 的排列十分有规律，因此我们可以将其转化为数组，不再需要链来链接它。

对于数组任一位置 \(i\) 上的元素，其左右儿子分别在在位置 \(2i + 1\) 和 \(2i +2\) 上，而它的父亲则在位置 \(\lfloor(i - 1)/2\rfloor\) 上。当然如果根从 \(1\) 开始，那么位置 \(i\) 上元素的左右儿子的位置分别为 \(2i\) 和 \(2i + 1\) ，而父亲的位置是 \(\lfloor i/2 \rfloor\) 。以下未说明的情况，我们将 1 作为 root 的下标。

堆序性质

保证 heap 可以快速执行的是 堆序性质 (heap-order property)。我们希望找到的是最小的元素，因此最小的元素在根上，而它的任一子树也是 heap，那么可以得出任一结点小于其所有后裔，这种结构被称为 小顶堆 (min heap)；而相反的，任一结点大于其所有后裔，则被称为 大顶堆 (max heap)。

heap-order 保证我们可以在 \(\mathcal{O}(1)\) 的时间复杂度内找到想要的元素。

堆的操作

如果我们希望对 heap 做一些操作，可能会破坏 heap-order property，所以我们应该保证无论如何操作，都可以恢复其性质。

binary heap 的插入操作

要在堆中插入一个元素，我们首先需要在尾部建立一个空穴，用以存放元素。为了不破坏 heap-order，我们比较插入元素与其父结点元素：如果元素可以放入空穴则插入完成，否则将父结点放入空穴，空穴转变为了父结点，自底向上递归直到元素插入。

这个过程被称为上滤 (percolate up)。percolate up 的最坏时间复杂度是 \(\mathcal{O}(\log_{}{N})\) ，这是需要 percolate up 到 root。但是平均来看， percolate up 的结束要早得多，平均需要 2.607 次比较，因此元素平均上移 1.607 层，平均时间复杂度 \(\mathcal{O}(1)\) 。

这里给出向堆中插入的元素的代码。有一个小技巧，交换元素需要三条赋值语句，如果 percolate up n，则需要 \(3n\) 条赋值语句，采用直接赋值覆盖的方法，则只需要 \(n + 1\) 次赋值。

1
2
3
4
5
6
7
8
9


template <class Comparable>
void insert(heap& h, Comparable x) {
  int hole = ++h.cur_size;
  while (hole > 1 && x < h[hole / 2]) {
    h[hole] = h[hole / 2];
    hole /= 2;
  }
  h[hole] = x;
}

binary heap 的移除操作

找出目标元素显然简单的多，因为 root 就是目标，但是如何将其从 heap 中移除。我们依然采取建立空穴的方法，只不过这次空穴建立在了 root。

我们进行与 percolate up 类似的操作，只不过这次从上向下进行，这被称为下滤 (percolate down)。我们从 root 出发，将孩子中的较小元素移动到空穴，并继续向下找去，直到空穴成为 leaf。到达 leaf 后，我们将最后一个结点值赋值给空穴，并删除最后一个结点，这样就能让 heap 的长度减一。

在实现时我们需要注意一个细节，当 heap 中元素的数量为偶数时，有的结点可能只有一个孩子。有一个小技巧，可以将一个大于任何 heap 元素的标识放在末尾，这样我们可以假设所有结点都有两个孩子，当然请小心处理。percolate down 的最坏与平均复杂度都是 \(\mathcal{O}(\log_{}{N})\) 的。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


void erase(heap& h) {
  auto tmp = h[h.cur_size--];
  int hole = 1;
  while (hole * 2 <= h.cur_size) {
    int child = hole * 2;
    if (child != h.cur_size && h[child + 1] < h[child]) {
      ++child;
    }
    if (h[child] < tmp) {
      h[hole] = h[child];
    } else {
      break;
    }
  }
  h[hole] = tmp;
}

binary heap 的其他操作

可以明确，min heap 中对查找最大元素并没有帮助，最大的元素在 leaf 上，但有半数的元素都是 leaf。在 heap 中我们不得不进行线性查找才能获取到特定元素。

当然我们还可以在 heap 上进行其他操作。

decrease_key(p, delta) ：将位置 p 的元素减小 \(\delta\) 。这有可能破坏 heap-order，因此需要对其进行 percolate up。
increase_key(p, delta) ：将位置 p 的元素增加 \(\delta\) 。这有可能破坏 heap-order，因此需要对其进行 percolate down。
remove(p) ：将位置 p 的元素移除。
build_heap ：通过原始集合构建一个堆，这个过程也被称为堆化 (heapify)。这个过程的平均运行时间是 \(\mathcal{O}(N)\) 的，最坏时间复杂度是 \(\mathcal{O}(N\log_{}{N})\) 的。

d 堆

binary heap 的实现简单，因此大部分时候 priority queue 优先使用其作为实现。d 堆 (d-ary heap) 是 binary heap 的简单推广，其每个结点总有 d 个孩子。所以简单的说， binary heap 就是一种 2-堆。

当然我们可以继续使用一个数组表示 d-ary heap，但是找出 node 和 parent 的乘法和除法都有个因子 d，因此更好的做法是使用 \(d = 2^{x}\) ，这样可以使用位运算加速除法过程。

一个显而易见的结论，当 d 增大时，其深度也将减少，因此 insert 时间复杂度是 \(\mathcal{O}(\log_{d}{N})\) ，但 erase 操作就会费时很多，erase 的时间复杂度是 \(\mathcal{O}(d\log_{d}{N})\) 。当然在 insert 远多于 erase 的算法中，d-ary heap 可以有效降低时间复杂度。不过实践证明，4-ary heap 可以胜过 binary heap。

左式堆

设计一种像 binary heap 又能以 \(\mathcal{O}(N)\) 的时间复杂度处理 merge，并且只使用一个数组的堆结构是困难的。因此大部分需要有效合并的数据结构都是链式的，但这可能导致其他操作变慢。

左式堆 (leftist heap) 像 binary heap 那样既有结构性质又有 heap-order property，不过所有的堆其 heap-order property 都是一样的，所以我们只需要关注它的结构性质。 leftist heap 也是二叉树，但区别是：leftist heap 并不是理想平衡的，而是趋于非常不平衡的。

左式堆的性质

将任一结点 X 的 零路径长 (null path length) \(npl(X)\) 或 \(s(X)\) 定义为从 X 到一个布局有两个孩子的结点的最短路径长。因此具有 \(degree = 0 \lor 1\) 的结点 \(npl = 1\) ，而 \(npl(null) = 0\) ，任意结点的 NPL 比其所有孩子的 NPL 的最小值加 1。对于 heap 中的每一个结点 X，左孩子的 NPL 至少与右孩子的 NPL 相等，这样树的结构更偏向于向左子树添加深度，因此称之为 leftist heap。

在右路径上有 r 个结点的左式树必然至少有 \(2^{r} - 1\) 个结点，而 N 个结点的左式树有一条右路径最多含有 \(\lfloor\log_{}{(N+1)}\rfloor\) 个结点。在左式堆上的操作，将所有工作都放在右路径上进行，以保证树不会过深。

左式堆的操作

leftist heap 中的基本操作是合并，而插入、移除是合并的特殊情形。插入元素可以看作是一个大堆和一个只有根结点的堆进行合并；移除元素时我们将会得到两个堆，将这两个堆进行合并即可得到新的 heap。

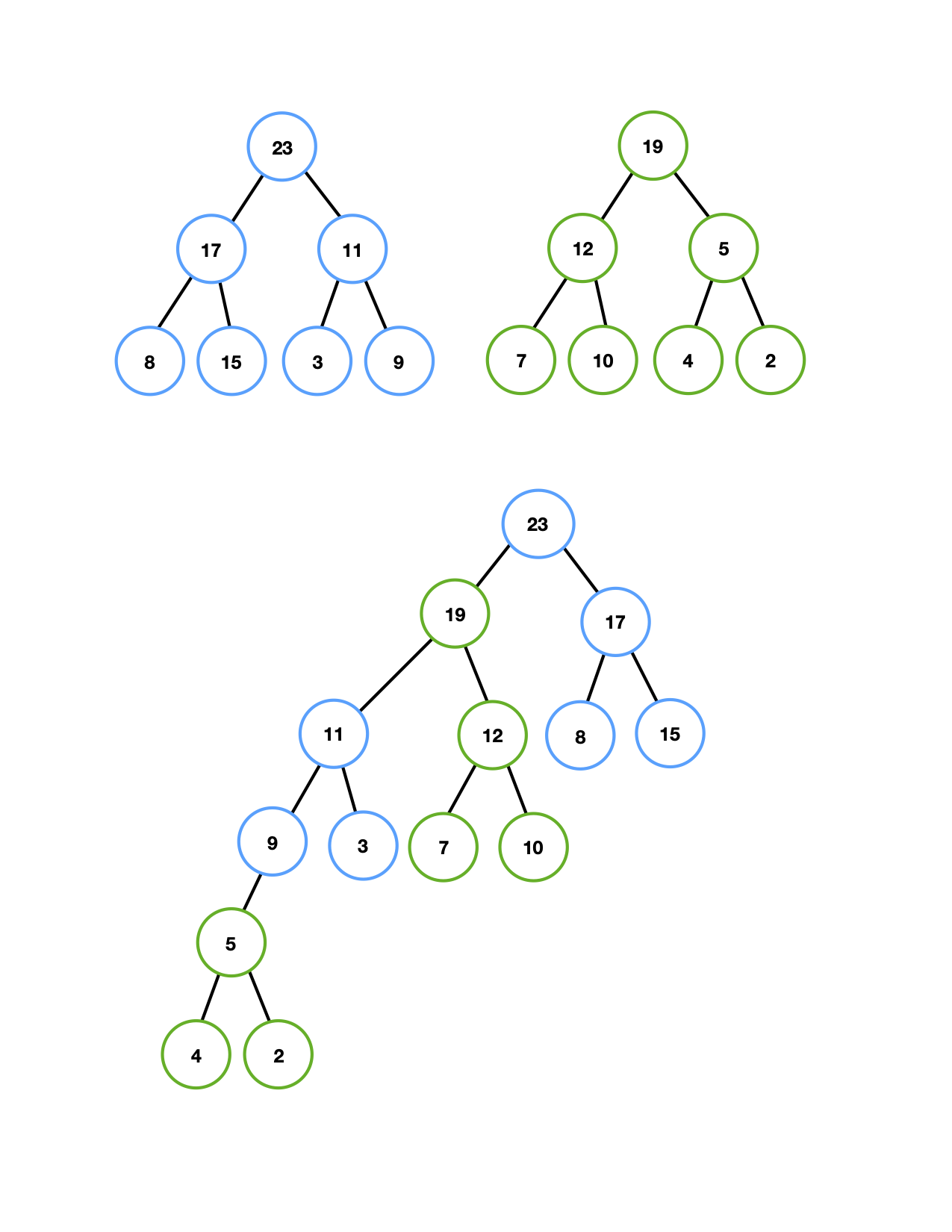
在合并时，递归地将 具有大的根值的堆 与 具有小的根值的堆 的 右子树 合并，如果右子树的 NPL 大于左子树的 NPL，则将两棵子树交互，以满足 leftist heap 的性质要求。

执行合并的时间与右路径的长度成正比，而递归调用时，每一个被访问的结点执行常数工作量，因此合并 leftist heap 的时间界为 \(\mathcal{O}(\log_{}{N})\) 。以下代码展示了合并操作的递归实现，如果你希望使用 loop 进行实现可能会有些困难，但可以肯定的是无论如何实现其结果等价。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


BinaryTreeNode* merge_impl(BinaryTreeNode* h1, BinaryTreeNode* h2) {
  BinaryTreeNode* merge(BinaryTreeNode* h1, BinaryTreeNode* h2); // 声明 merge 函数
  if (h1->left == nullptr) {
    h1->left = h2;
    return h1;
  }
  h1->right = merge(h1->right, h2);
  if (get_npl(h1->left) < get_npl(h1->right)) {
    swap(h1->left, h1->right);
  }
  set_npl(h1, 1 + get_npl(h1->right));
  return h1;
}
BinaryTreeNode* merge(BinaryTreeNode* h1, BinaryTreeNode* h2) {
  if (h1 == nullptr) {
    return h2;
  }
  if (h2 == nullptr) {
    return h1;
  }
  return h1->data < h2->data ? merge_impl(h1, h2) : merge_impl(h2, h1);
}

斜堆

斜堆 (skew heap) 是 leftist heap 的自调节形式，skew heap 与 leftist heap 的关系类似于 AVL tree 与 splay tree 之间的关系。skew heap 不对树的结构进行限制，右路径可以任意长，因此所有操作的最坏运行时间为 \(\mathcal{O}(N)\) 。但是正如 splay tree，它的 amortized 运行时间为 \(\mathcal{O}(\log_{}{N})\) 。skew heap 的基本操作也是合并，且操作与 leftist heap 是类似的，唯一的不同是 skew heap 不再存储 NPL，交换孩子是无条件的。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


BinaryTreeNode* merge_impl(BinaryTreeNode* h1, BinaryTreeNode* h2) {
  BinaryTreeNode* merge(BinaryTreeNode* h1, BinaryTreeNode* h2); // 声明 merge 函数
  h1->right = merge(h1->right, h2);
  swap(h1->left, h1->right);
  return h1;
}
BinaryTreeNode* merge(BinaryTreeNode* h1, BinaryTreeNode* h2) {
  if (h1 == nullptr) {
    return h2;
  }
  if (h2 == nullptr) {
    return h1;
  }
  return h1->data < h2->data ? merge_impl(h1, h2) : merge_impl(h2, h1);
}

二项队列

二项队列不同于前面介绍的所有优先队列的实现，其是堆序的树的集合，称为森林。森林中的每一棵 二项树 (binomial tree) 都是有约束的堆序树，每一个高度上至多存在一棵二项树，高度为 0 的二项树是一颗单结点树；高度为 k 的二项树 \(B_k\) 通过将一棵二项树 \(B_{k-1}\) 附接到另一棵二项树 \(B_{k-1}\) 的根上构成。

高度为 k 的二项树恰好有 \(2^k\) 个结点，而深度 d 处的结点树是二项系数 \[\left(\begin{aligned} k \\ d \end{aligned}\right).\]

如果将堆序施加于二项树上，并允许任意高度上最多一棵二项树，那么能够用二项树的集合唯一地表示任意大小的优先队列。例如，大小为 13 的优先队列可以用森林 \(B_3\) 、\(B_2\) 、\(B_0\) 表示，将这种二项队列写作 \(1101\)。

二项队列操作

最小元可以通过搜索所有树的根找出，最多有 \(\log_{}N\) 棵不同的树，因此最小元可以以 \(\mathcal{O}(\log N)\) 时间找出。若记住当最小元在其他操作期间变化时更新它，那么可以保留最小元的信息并以 \(\mathcal{O}(1)\) 时间执行操作。

合并两个二项队列在概念上很容易，对于两个同高度的二项树可以合并为更高的树，让值大的根成为值小的根的子树。有时合并后，可能出现三棵高度相同的树，在两个队列中各取一棵继续合并即可。直到没有高度相同的树为止，合并结束。

插入可以看作合并的特殊情况，创建一棵单结点树，然后执行合并即可。删除操作由找到具有最小根的二项树来完成，将该树先从森林中移除，删除掉根后，拆解为新的二项队列，最后合并这两个队列即可。

二项队列的实现

为了保证快速合并，可以按高度大小递减的顺序保存这些二项树的根。而二项树的结点，可以像树一样存储，一个儿子指针域，一个兄弟指针域，和一个元素域。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


struct BinomialNode {
  Comparable element;
  BinomialNode* child;
  BinomialNode* sibling;
  BinomialNode(const Comparable& e, BinomialNode* c, BinomialNode* s)
      : element(e), child(c), sibling(s) {}
};

class BinomialQueue {
 private:
  int size;
  vector<BinomialNode*> forest;
 public:
  BinomialQueue() = default;
};

合并两个二项队列的实现，首先需要确定如何合并两棵同高度的树。

1
2
3
4
5
6
7
8


BinomialNode* merge_tree(BinomialNode* t1, BinomialNode* t2) {
  if (t2->element < t1->element) {
    return merge(t2, t1);
  }
  t2->sibling = t1->child;
  t1->child = t2;
  return t1;
}

对于实现合并操作，在任意时刻，仅处理高度为 i 的那些树，并且始终从高度最低的树开始像最高的树合并。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61


// 将二项队列 B 合并到 A，并清空 B
void merge(BinomialQueue& a, BinomialQueue& b) {
  a.size += b.size;
  if (a.size > a.capacity()) {
    int old_forest_size = a.forest.size();
    int new_forest_size = max(old_forest_size, b.forest.size()) + 1;
    a.forest.resize(new_forest_size);
    for (int i = old_forest_size; i < new_forest_size; ++i) {
      a.forest[i] = nullptr;
    }
  }
  BinomialNode* carry = nullptr;
  for (int i = 0, j = 1; j <= a.size; ++i, j *= 2) {
    BinomialNode* t1 = a.forest[i];
    BinomialNode* t2 = i < b.forest.size() ? b.forest[i] : nullptr;
    int which_case = t1 == nullptr ? 0 : 1;
    which_case += t2 == nullptr ? 0 : 2;
    which_case += carry == nullptr ? 0 : 4;
    switch (which_case) {
      case 0: {  // no tree
        [[fallthrough]];
      }
      case 1: {  // only t1
        break;
      }
      case 2: {  // only t2
        a.forest[i] = t2;
        b.forest[i] = nullptr;
        break;
      }
      case 3: {  // t1 and t2 exist
        carry = merge_tree(t1, t2);
        a.forest[i] = b.forest[i] = nullptr;
        break;
      }
      case 4: {  // Only carry
        a.forest[i] = carry;
        carry = nullptr;
        break;
      }
      case 5: {  // t1 and carry exist
        carry = merge_tree(t1, carry);
        a.forest[i] = nullptr;
        break;
      }
      case 6: {  // t2 and carry exist
        carry = merge_tree(t2, carry);
        b.forest[i] = nullptr;
        break;
      }
      case 7: { // all exist
        a.forest[i] = carry;
        carry = merge_tree(t1, t2);
        b.forest[i] = nullptr;
        break;
      }
    }
  }
  b.forest.clean();
  b.size = 0;
}

目录

堆结构

模型

二叉堆