散列表

She made a hash of the proper names, to be sure.

— Grant Allen

散列函数

如果可以将存储的数据，其中某一项用于查找，则这个项被称为 键 (key)，而通过一定规则将键映射到表中的一个合适的单元，这个规则被称为 散列函数 (hash function)。我们希望 hash 足够简单且保证两个不同的 key 映射到不同的单元，但是单元是有限的，因此我们需要寻找一个 hash function 尽量均匀的产生 hash value。当映射不是单射而是多射时，即发生了 冲突 (collision)，有两个不同的 key 经过 hash function 得到了相同的 hash value，我们应该处理这个 collision。

顺便一提，我们一般使用 hash value 对表长进行取模，从而确定数据在表中的位置，表长为素数是可以很好的让 hash value 取模后均匀分布在表中。

我们假设一个简单的字符串 hash function，即将字符串中所有的字符的 ASCII 相加所得到的。如果表很大，就不能很好的平均分配数据。比如 \(TableSize = 10'007\) ，并设所有的键长度为 8，而这些键的最大 hash value 不超过 1016 (\(127 * 8\))，这显然不是平均分配的。

如果假设 Key 至少有 3 个字符，并且设置一个只考虑前 3 个字符的 hash function： \(c_{0} + 27 * c_{1} + 27 * 27 * c_{2}\) 。我们假设键的前三个字符是随机的，表的大小依然是 10007，那么我们就会得到一个均匀分布的 hash value。但是英文实际上并不是随机的，虽然前三个字符有 \(26^{3} = 16576\) 种可能的组合，但是事实证明 3 个字母不同的组合数实际上只有 2851 。

再列出最后一个简单的 hash function： \[\sum_{i=0}^{length-1}{Key[length-i-1] * 37^{i}}.\] 这将使用 key 中的所有字符，计算一个关于 \(37\) 的多项式。可以发现利用这个 functino 需要修正其值可能为负，因为 hash value 计算过程中可能会存在溢出。

这是一个不错的算法，但并不完美，如果键过长的话可能导致计算时间的增加，你可以使用奇数位字符或者其他方法来优化函数。选定了 hash function，那么接下来的主要问题就是如何解决 collision。

分离链接法

分离链接法 (separate chaining) 也被称为拉链法，这种做法是将散列到同一个值的所有元素保存到一个链表中，或者一个 BST 甚至另一个散列表。

我们假定散列表的 装填因子 (load factor) \(\lambda\) 为散列表中的元素个数与散列表大小的比值。执行一次查找操作所需要的工作是：计算散列函数值 (\(\mathcal{O}(1)\)) 并遍历冲突所组成的表。在一次不成功的查找中，要访问的结点数平均为 \(\lambda + e^{-\lambda} \approx \lambda\) ；成功的查找则需要遍历大约 \(1 + (\lambda / 2)\) 个链。

被搜索的表包含了一个存储匹配的结点再加上 0 或更多其他的结点，因此在 N 个元素的表以及 M 个链表中，其他结点的期望个数为 \((N - 1) / M = \lambda - 1 / M\) ，当 M 很大时可以认为这就是 \(\lambda\) 。因此可以发现，散列表的大小并不重要，重要的是元素的 load factor。使用 separate chaining 时，我们往往认为 \(\lambda \approx 1\) 最好，当 \(\lambda > 1\) 时我们就扩展表并对其中的元素进行 再散列 (rehash)。

不使用链表的散列表

由于 separate chaining 需要使用链表，给新单元分配地址可能需要额外的时间，并且还要求第二种数据结构的实现，因此另一种解决方法是将 collision 发生时尝试选择另一个单元，直到找到空白单元为止。

更正式的表达方式是： 单元 \(h_{0}(x), h_{1}(x), \cdots\) 一次进行尝试，其中 \(h_{i}(x) = (hash(x) + f(i)) mod Length_{table}\) 且 \(f(0) = 0\) 。函数 \(f\) 是冲突解决函数。因为所有的数据都要放在表内，因此所需要的表就远大于 separate chaining 的表。我们将这种方案称之为 探测散列表 (probing hash tables)，而 probing hash 的 \(\lambda\) 一般来说应该低于 \(0.5\)。

线性探测

线性探测时 \(f\) 是关于 \(i\) 的线性函数，一般情况下 \(f(i) = i\) ，即当冲突发生时从下一个单元开始依次测试是否为空单元，直到找到相应空单元为止。

我们以序列 {89, 18, 49, 58, 69} 为例，散列函数为 \(f(i) = i \mod 10\)：前两次插入都是开放单元，直接插入即可；插入 49 时将与 89 发生冲突，将其放入下一开放地址 0 中；插入 58 时将先后与 18、89、49 发生冲突，最终经过三次比较落入开放地址 1 中；等等。

由此可见当表足够大时，总能找到一个开放单元，但需要花费相当多的时间。更糟的是，即使表较为空，这些占据的单元也会形成一些区块，其结果被称为 一次聚集 (primary clustering)。于是，需要尝试多次才能解决冲突。线性探测的预期探测次数对于插入和不成功的查找来说，大约需要 \(\frac{1}{2}(1 + 1 / (1 - \lambda)^{2})\) ，对于成功的查找来说则是 \(\frac{1}{2}(1 + 1 / (1 - \lambda))\) 。

在 Weiss 的书中为我们介绍了如何使用积分计算插入时间平均值的方法来估计平均值，并将线性探测的性能与其他更随机的方法的期望性能做了比较，如下图所示。

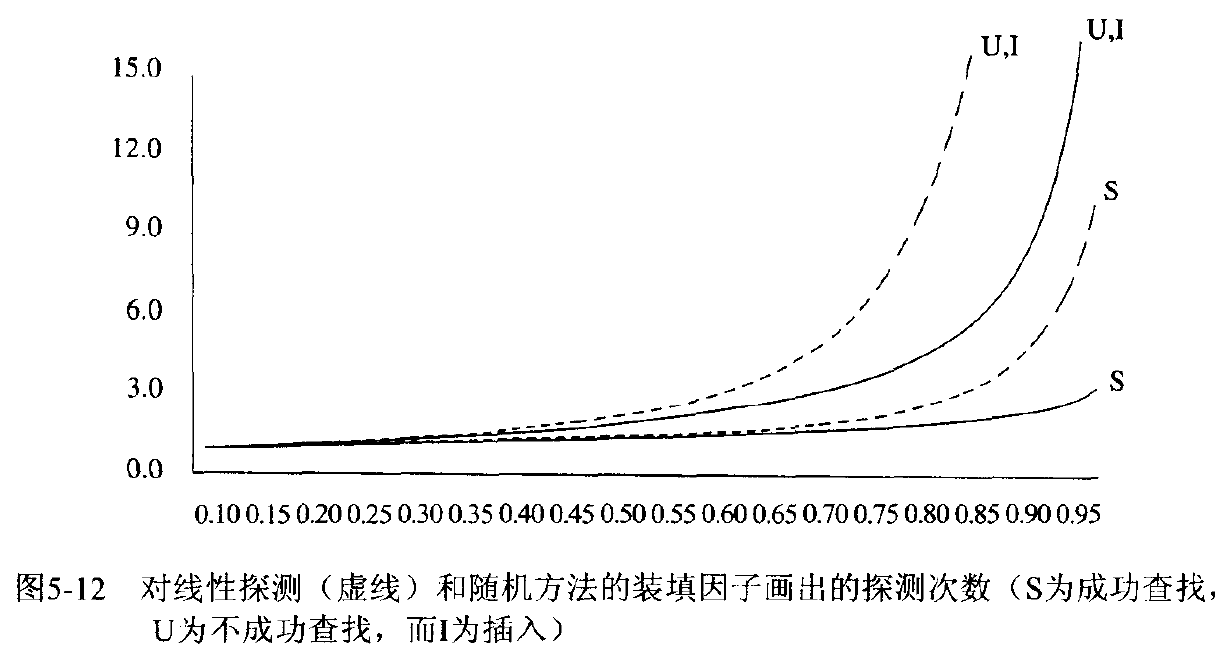
可以看到如果 \(\lambda = 0.75\) 时，使用线性探测进行插入预计需要 8.5 次探测；如果 \(\lambda = 0.9\) 时，则需要 50 此探测；而 \(\lambda = 0.5\) 时，平均插入操作只需要 2.5 次探测，成功的查找平均需要 1.5 次探测。

平方探测

平方探测是消除线性探测中 primary clustering 的解决方法，探测函数 \(f\) 是关于 \(i\) 的二次函数，一般情况下 \(f(i) = i^{2}\) 。

我们以相同的序列为例：当 49 与 89 冲突时，其下一个位置是一个开放单元，49 就被放置在这里；58 先后与 18、89 发生冲突，然后探测位置 \((8 + 2^{2})\,mod\,10\) ，由于该位置是开放的单元，因此 58 就放在这里。

对于平方探测来说，散列表被近乎填满是一个糟糕的情况：当表被填满超过一半时，若表的大小不是素数，甚至可以在表未被填满一半前，就不能保证找到空单元了。因为最多只有一般的表可以用作被选单元。但是如果表的大小是素数，那么在表至少有一半是空的时候，总能够插入一个新的单元。

如果哪怕表有比一半多一个的位置被填满，那么插入都有可能失败 (虽然这种可能性很小)。另外如果表的大小是素数 (形如 \(4k + 3\))，且使用的探测函数为 \(f(i) = \pm i^{2}\) ，那么整个表均可以被探测到。如果不是素数大小的表，那么备选单元的个数会极大的减少。

虽然平方探测排除了 primary clustering，但是散列到同一位置的元素将探测相同的备选单元，这被称为 二次聚集 (secondary clustering)。幸运的是，预期探测次数对于插入和不成功的查找来说，大约需要 \(1 / (1 - \lambda)\) ，对于成功的查找来说则是 \(-\frac{1}{\lambda}\ln(1 - \lambda)\) 。

顺便一提，如果在使用 probing 方案的 hash table 中需要删除一个元素，那么不能直接删除这个元素，而是需要惰性删除，否则可能造成查询操作失败。

双散列

双散列 (double hashing) 是准备另一个 hash function，而探测函数 \(f\) 是关于 \(i\) 与第二个 hash function 的函数，一般情况下 \(f(i) = i * hash_{2}(x)\) 。对于这种方法，如果第二个 hash function 选择的并不好，则会有很大的问题，需要保证运算结果不为 0 且所有单元都可以被检测到。诸如 \(hash_{2}(x) = R - (x\,mod\,R)\) (R 是小于 Len 的素数) 这样的函数可以取得不错的效果。

双散列预期的探测次数与随机冲突解决方法的情形相同，在理论上这十分有吸引力，但备选单元可能提前用完，而平方探测的实现更简单且效率更高。

再散列

对于 \(\lambda\) 超过一定比例的散列表来说，我们需要对其进行扩容，与顺序实现的现行表类似，一般扩容倍数选择在 1.5 或 2 倍，从采用一个相关的新 hash function。之后需要扫描原始散列表，并计算所有未删除的元素的新散列值，插入到新表中。整个操作过程被称为 再散列 (rehashing)。

rehashing 的操作无疑是昂贵的，它需要 \(\mathcal{O}(N)\) 的时间复杂度。不过幸运的是这并不常发生，而且 rehashing 时表中必然已存在 \(N / 2\) 个元素，均摊到每个元素的插入上，基本的开销是一个常数。

当然再散列也可以有不同的策略，最常见的就是在表到达一半时就 rehashing，当然也可以当插入失败时才进行 rehashing。还有一种 途中 (middle-of-the-road) 的策略：当表到达某个 load factor 时进行 rehashing。可以肯定的是，随着 load factor 的增加，表的性能在下降，因此选择一个好的截止点可能是最好的策略。

可扩散列

在上一篇文章中，讲解了针对将数据存储于磁盘当中的 B 树，现在我们需要思考如何将散列表存储于磁盘当中。我们依然需要考虑的是检索数据时所需的磁盘读取次数。

假设有这样的前提：任意时刻都有 N 个记录要存储，N 随时间变化而变化；最多可以把 M 个记录放入一个磁盘区块。我们假设 \(M = 4\) 。

如果使用 separate chaining 或 probing hashing，即使是理想分布的散列表，在一次查询操作中，都可能因冲突而引起对多个区块的访问。当表变得过满时，必须 rehashing 用 \(\mathcal{O}(N)\) 的巨大代价来访问磁盘。

一种聪明的方法是 可扩散列 (extendible hashing)，它允许用两次磁盘访问执行一次查找，插入操作也需要很少的磁盘访问。这种算法与 B 树的思想相当。