iris
归档 标签 分类 系列 关于 友人帐
iris

控制流、递归、高阶函数

GinShio  收录于  类别 Programming 和 系列 CS61A Note
     约 3746 字   预计阅读 8 分钟 
系列 - CS61A Note

解释器所执行语句来执行某些操作。

比如这整个复合语句 (compound statement)，在 Python 中由 def 声明；标头 header 确定了一个简易语句 (clause) 的类型，这个语句中跟随了一个语句序列 (suite)。解释器会按一定顺序执行这个语句序列。

条件语句在大部分语言中以 if 关键字呈现。

在 Python 中 True 和 False 分别表示真或假，if 引导条件语句及其真分支，零或一个 else 引导假分支，其中还可能会有零或多个 elif 进行嵌套。

1
2
3
4
5
6
7

def absolute_value(n):
    if n < 0:
        return -n
    elif n == 0:
        return 0
    else:
        return n

在 scheme 中 #t 和 #f 分别表示真或假，语法的话就不能 elif 进行嵌套了 (if test consequent alternative)

1
2

(define (absolute-value n)
  (if (positive? n) n (- n)))

FP 中一般都会提供一套类似 guard 的语法，即该条件语句可以接受任意多的条件判断，由上至下进行条件判断，在条件为真时执行语句块并退出条件语句，如果所有条件都不符合将有一个默认块进行兜底处理。其实这个语句更像是 if-then-elif-else 的变体。

1
2
3

(cond ((< n 0) (- n))
      ((= n 0) n)
      (else n))

在 erlang 中，if 就是 cond。

1
2
3
4
5
6

absolute_value(N) ->
    if
        N < 0 -> -N;
        N =:= 0 -> N;
        true -> N
    end.

迭代语句也称循环语句，在满足条件的情况下运行循环体，直到不满足的情况下退出。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

i = 0
total = 0
while i < 3:
    total = total + i
    i = i + 1
    print(total)

print(total)
# 0
# 1
# 3

scheme 中的循环与正常语言中的 while 差距有点大，虽然更像是 C 语言中的 for (也可能是 C 的 for 更像是 lisp 的 do)，无论怎么说，都是一种带变量变化的循环语句。

1
2
3
4
5
6
7
8

(do ((i 0 (+ i 1)) (total 0 (+ total i))) ;; assignment
    ((> i 2) total) ;; exit
  (display total) ;; body
  (newline))
;; 0
;; 0
;; 1
;; 3 -- not print

erlang 作为一种 pure 的 FP 并没有可用的 while 语句，需要使用尾递归来模拟。

1
2

loop(3, Total) -> Total;
loop(I, Total) -> loop(I + 1, Total + I).

质因数分解是一个典型的需要用循环、条件来查找出答案的问题。对于每个正整数 N，我们都可以分解出它的所有质因数集合：

  • 8 = 2 * 2 * 2
  • 9 = 3 * 3
  • 10 = 2 * 5
  • 11 = 11
  • …

比较好的一种方式是，寻找这个正整数的最小质因数，之后再继续分解剩余的部分，直到分解完成。 \[858\ =\ 2 * 429\ =\ 2 * 3 * 143\ =\ 2 * 3 * 11 * 13.\]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

(define (get-primes n)
  (let ((bits (make-vector (+ n 1) #t)))
    (let loop ((p 2) (ps '()))
      (cond ((< n p) (reverse ps))
            ((vector-ref bits p)
             (do ((i (+ p p) (+ i p))) ((< n i))
               (vector-set! bits i #f))
             (loop (+ p 1) (cons p ps)))
            (else (loop (+ p 1) ps))))))

(define (get-factorization n primes)
  (let ((prime (car primes))
        (others (cdr primes)))
    (if (= (remainder n prime) 0)
        prime
        (get-factorization n others))))

(define (prime-factorization n)
  (if (< n 3)
      (list n)
      (let ((primes (get-primes n)))
        (let loop ((num n) (ans '()))
          (cond ((= num 1) (reverse ans))
                (else (let ((prime (get-factorization num primes)))
                        (loop (quotient num prime) (cons prime ans)))))))))

递归 (Recursion) 在数学与计算机科学中，是指在函数的定义中使用函数自身的方法。递归一词还较常用于描述以自相似方法重复事物的过程。例如，当两面镜子相互之间近似平行时，镜中嵌套的图像是以无限递归的形式出现的。也可以理解为自我复制的过程。

以下是一个可能更有利于理解递归过程的解释：

  1. 我们已经完成了吗？如果完成了，返回结果。如果没有这样的终止条件，递归将会永远地继续下去。
  2. 如果没有，则简化问题，解决较容易的问题，并将结果组装成原始问题的解决办法。然后返回该解决办法。

\[\begin{aligned} Factorial(0) &= 1,\\ Factorial(1) &= 1,\\ Factorial(N) &= N \times Factorial(N - 1). \end{aligned}\]

1
2
3

(define (factorial n)
  (cond ((= n 0) 1)
        (else (* n (factorial (- n 1))))))

这个计算过程中，通过代换模型可以看出计算是一种先逐步展开而后收缩的形状，计算过程构造起一个推迟进行的操作所形成的链条，收缩阶段表现为这些运算的实际执行，这种计算过程被称为递归计算过程。如果要执行这个过程，解释器就必须维护好以后要执行的操作的轨迹，这个例子中推迟执行的乘法链条的长度也就是为保存其轨迹需要保存的信息量，这个长度随着 n 值的增加而线性增长，这个过程被称为线性递归计算。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

(factorial 5)
(* 5 (factorial 4))
(* 5 (* 4 (factorial 3)))
(* 5 (* 4 (* 3 (factorial 2))))
(* 5 (* 4 (* 3 (* 2 (factorial 1)))))
(* 5 (* 4 (* 3 (* 2 (* 1 (factorial 0))))))
(* 5 (* 4 (* 3 (* 2 (* 1 1)))))
(* 5 (* 4 (* 3 (* 2 1))))
(* 5 (* 4 (* 3 2)))
(* 5 (* 4 6))
(* 5 24)
120

来看另一种实现

1
2
3
4
5
6

(define (factorial n)
  (let factorial-iter ((product 1) (counter 1))
    (if (> counter n)
        product
        (factorial-iter (* counter product)
                        (1+ counter)))))

这个计算过程中没有任何增长或收缩，计算过程的每一步，需要保存的轨迹就是变量 product 和 counter 的当前值，我们称这个过程为迭代计算过程。迭代计算过程就是那种其状态可以用固定数目的状态变量描述的计算过程，同时又存在一套固定的规则描述了计算过程从一个状态到另一个状态转换时状态变量的更新方式，还有一个结束状态的检测用以描述计算过程如何终止。

1
2
3
4
5
6
7

(factorial-iter   1 1 5)
(factorial-iter   1 2 5)
(factorial-iter   2 3 5)
(factorial-iter   6 4 5)
(factorial-iter  24 5 5)
(factorial-iter 120 6 5)
120

\[\begin{aligned} Fibonacci(0) &= 0,\\ Fibonacci(1) &= 1,\\ Fibonacci(N) &= Fibonacci(N - 1) + Fibonacci(N - 2). \end{aligned}\]

可以看出斐波那契数列是一个天然递归的函数，函数递归在之前的代码中已经遇到了，直接看代码实现。

1
2
3
4
5

(define (fibonacci n)
  (cond ((= n 0) 0)
        ((= n 1) 1)
        (else (+ (fibonacci (- n 1))
                 (fibonacci (- n 2))))))

如果将 fibonacci 函数的调用图画出来，可以看到它就像一棵树一样，这样的递归被称为 树形递归。但是其中有大量的重复计算，会导致无意义的计算从而浪费 CPU 的性能。

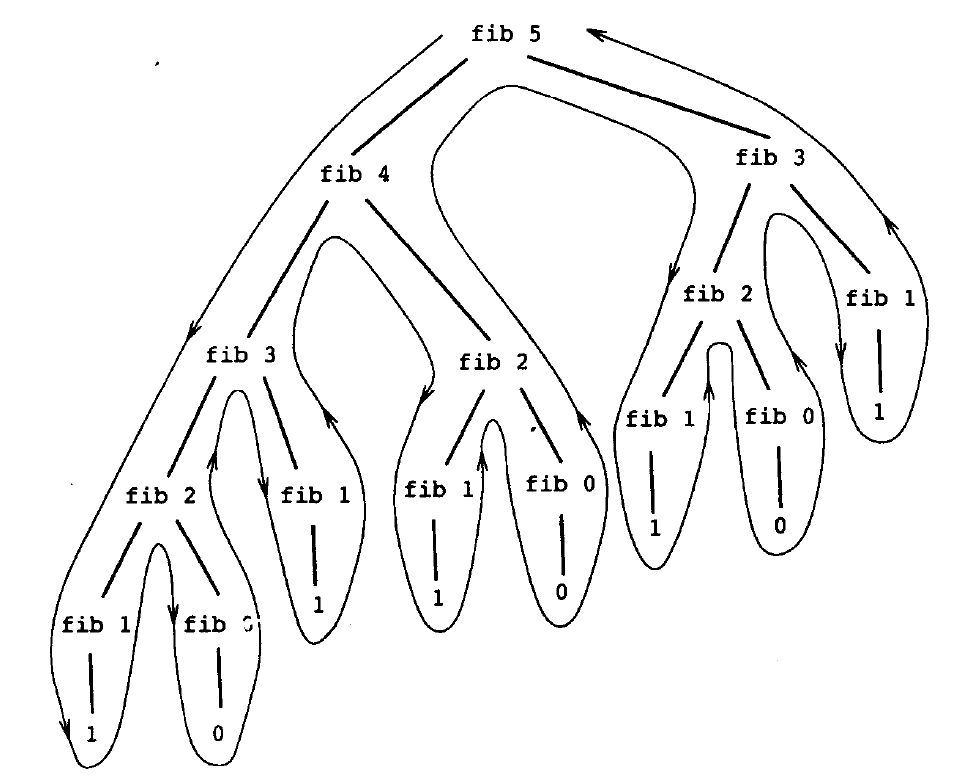
由于这种计算斐波那契数列的方法很糟糕，做了很多冗余计算，其递归次数跟随 n 的大小指数增加，因此我们需要使用迭代的方法来优化这个求解过程。

1
2
3
4
5

(define (fibonacci n)
  (let fibonacci-iter ((a 1) (b 0) (counter 1))
    (if (> counter n)
        b
        (fibonacci-iter (+ a b) a (+ counter 1)))))

树形递归计算过程并不是无用的，当考虑在层次结构性的数据上操作，而不是对数操作时，树形递归计算过程是一种自然、威力强大的工具，可以帮助我们理解与设计程序。

如果不能直接使用取模的方法判断奇偶数，那么有一个简单且明了的方式 – 询问前一个数是否是奇 / 偶数。显然这是个递归问题，我们需要不断向前询问，直到得到答案。

1
2
3
4
5
6
7
8

(define (odd? n)
  (if (= n 0)
      #f
      (even? (- n 1))))
(define (even? n)
  (if (= n 0)
      #t
      (odd? (- n 1))))

这种有多个函数互相递归调用的方式，称其为间接递归。

高阶函数 (Higher-Order Functions) 是一类将函数作为参数、返回值进行传递的函数，这种特性多发生在具有 FP 特性的语言中，往往这些语言还会同时提供 lambda。

lambda 表达式 是一种简化的定义函数的方式，可以捕获当前环境中的一些变量，也被称为闭包 (clause)。lambda 往往伴随着高阶函数出现，通常是传递条件谓词时，创建一个对应的 lambda 对象，而不是创建一个函数传递。

1
2

(lambda (x)
  (= x 0))

lambda 与正常函数无异，由三部分组成 – 标头 (lambda 关键字)、参数列表和函数体组成。另外一点，lambda 无法递归，如果想要递归 lambda 需要使用 Y 组合子。1 , 2

lambda 中捕获的环境变量是可以直接使用的

1
2
3
4

(define (zero? x)
  ((lambda () (= x 0))))
(zero? 0) ;; #t
(zero? 1) ;; #f

对于一个函数，在设计一个函数时，需要注意三个方面：

  1. 每个函数应该只有一个精确的任务，执行多个任务的函数应该被拆分为多个函数
  2. 不要重复自己 (DRY, Don’t repeat yourself)，如果你发现自己在复制粘贴一段代码，你可能已经发现了一个机会用函数抽象
  3. 函数应该被设计的更通用，比如不提供 square 和 cube，而是提供 pow，指定幂来分别实现 square 和 cube

比如你现在需要计算累和，包括但不限于 \(\sum_{i=1}^{n}{i}\)、\(\sum_{i=1}^{n}{i^{2}}\) 等，根据设计函数的 3 个方面，我们需要设计一个用于累加的函数！另外，这个函数需要有足够的抽象，来提供泛用性。

那么我可以定义两个参数 start 和 end 用于标识累加函数的上下限，那么最重要的如何累加应该怎么告诉这个函数呢？将这个函数设计为高阶函数！

1
2
3
4
5
6
7
8

(define (summation start end term)
  (let summation-iter ((counter start) (value 0))
    (if (> counter end)
        value
        (summation-iter (+ counter 1) (+ value (term counter))))))
(summation 0 10 (lambda (x) x))  ;; sum (i), 55
(summation 0 10 (lambda (x) (* x x))) ;; sum (i^2), 385
(summation 0 10 (lambda (x) (sqrt x))) ;; sum (sqrt(i)), 22.4682

柯里化 (currying) 是数学和 FP 的重要特性，将接收多个参数的函数转换为接收一个参数的函数，并且返回接收余下的参数而且返回结果的新函数的技术。所以这三个表达式是等价的。

\[ \begin{align} x &= f(a, b, c)\\ & \left\{\begin{aligned} h &= g(a)\\ i &= h(b)\\ x &= i(c) \end{aligned}\right.\\ x &= g(a)(b)(c) \end{align}\] 
1
2
3
4
5

(define (sum a b) (+ a b))
(define (sum-curry a) (lambda (b) (+ a b)))
(define add10 (sum-curry 10))
(add10 5)  ;; 15
(sum 10 5) ;; 15

  • 计算排列

    数学概念排列 \(P_{k}^{n} = \frac{n!}{(n-k)!}\)，数学概念组合 \(C_{k}^{n} = \binom{n}{k} = \frac{P_{k}^{n}}{k!} = \frac{n!}{k!(n-k)!}\)。实现一个计算排列的函数

    1
2
3
4
5
6
7
8
9

    (define (falling n k)
  "Compute the falling factorial of n to depth k."
  (define factorial
    (lambda (n)
      (cond ((= n 0) 1)
            ((= n 1) 1)
            (else (* n (factorial (- n 1)))))))
  (/ (factorial n)
     (factorial (- n k))))

  • 计算整数 n 的每位数字之和

    1
2
3
4
5
6

    (define (sum-digits n)
  "Sum all the digits of y."
  (let sum-digits-iter ((num n) (val 0))
    (if (= num 0)
        val
        (sum-digits-iter (quotient num 10) (+ val (remainder num 10))))))

  • 查询整数 n 是否有两个连续的 8

    1
2
3
4
5
6
7
8

    (define (double-eights n)
  "Return true if n has two eights in a row."
  (let double-eights-iter ((num n) (prev #f))
    (if (= num 0)
        #f
        (let ((curr (= (remainder num 10) 8)))
          (or (and curr prev)
              (double-eights-iter (quotient num 10) curr))))))
product
计算 \(term(1) \times term(2) \times \cdots \times term(n)\) 
1
2
3
4
5
6

(define (product n term)
  "Return the product of the first n terms in a sequence."
  (let product-iter ((counter 1) (init 1))
    (if (> counter n)
        init
        (product-iter (+ counter 1) (* init (term counter))))))
accumulate
累加函数 
1
2
3
4
5
6
7
8

(define (accumulate merger init n term)
  "Return the result of merging the first n terms in a sequence and start.
    The terms to be merged are term(1), term(2), ..., term(n). merger is a
    two-argument commutative function."
  (let accumulate-iter ((counter 1) (value init))
    (if (> counter n)
        value
        (accumulate-iter (+ counter 1) (merger value (term counter))))))

I know! I’ll use my Higher-order functions to Order higher rolls.

在 Hog 中，两个玩家轮流尝试接近目标，成为第一个总分至少到达目标的玩家胜利，默认目标为 100 分。每次尝试，玩家选择至多十个色子进行投掷。玩家的得分是本轮所有骰子点数之和。一名玩家如果投掷太多骰子将会面临一定风险：

  • Sow Sad，如果任何骰子的结果为 1，则当前玩家的回合得分为 1。

在一局正常的 Hog 游戏中，这就是所有的规则了。为了增加一些游戏特色，我们将添加一些特殊规则：

  • Pig Tail，一名玩家如果选择投掷 0 个骰子，他将得 \(2 \times \lvert{tens - ones}\rvert + 1\) 分。其中 tens 和 ones 指对手分数的的十位数字和个位数字。

  • Square Swine，当一名玩家在他的回合获得了分数，且最终结果是一个完全平方数，那么将他的分数设置为下一个完全平方数。

  1. Why oh why Y? ↩︎

  2. 为什么是Y? ↩︎

更新于 10-03
阅读原始文档 | 报告问题
 Note, CS61A, SICP
返回 | 主页